MiHsC & emdrive: a new approach.

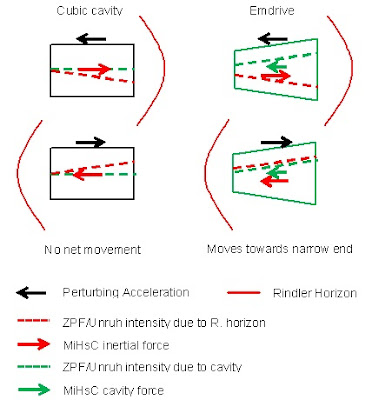
In previous work I've offered an explanation for emdrive in terms of MiHsC operating on the light within the emdrive cavity (see McCulloch, 2015), and I have not abandoned this photon based approach (I'm now convinced it is better, but might benefit from the diagram below). However, in the past couple of days I've wondered whether I can do it, probably with the same maths, by looking at the cavity instead and forgetting about the light, except as a source of vibration. This schematic shows what I have been considering.

It shows, on the left, a cubic cavity (black box) accelerated left (upper panel) and right (lower panel) by the microwaves in the cavity. In each case a Rindler horizon (red curve) appears in the opposite direction to the acceleration and MiHsC then damps the Unruh radiation more on that side (see the red dashed line which shows the decrease of power in the Unruh spectrum going towards the horizon, ie: the red line trends down). This gradient in the Unruh spectrum then pushes the cubic cavity in the opposite direction to whatever acceleration it had and thereby gives it inertia (McCulloch, 2013).

Now look at the emdrive cavity (right hand side). Again we accelerate it left and right, and again the Unruh radiation spectrum decreases towards the horizon making a force that counters the initial acceleration, but now the cavity itself, assuming it's like a horizon and MiHsC applies, also damps the Unruh radiation more at the narrow end (see the green dashed line, which shows decreasing power towards the narrow end). This then, for both left and right acceleration pushes the emdrive towards its narrow end. The acceleration is essential, because without it you wouldn't have the Unruh field and the cavity wouldn't be able to make it asymmetric.

This is a different way of thinking about it than using photons, but it uses MiHsC in the same way and cuts out having to worry about light which is difficult to visualise. Comments welcome!

References

McCulloch, M.E., 2013. Inertia from an asymmetric Casimir effect. EPL, 101, 59001. Link

McCulloch, M.E., 2015. Can the Emdrive be explained by quantised inertia? Progress in Physics, 11, 1, 78-80. Link.

Emdrive: whence motion?

Imagine an object in empty space accelerating rightwards. Now information from beyond a certain distance to its left, limited to light speed, can't catch up so there is an  information horizon, and the volume to the left of that horizon can never be seen by the object. A radiation like Hawking radiation comes off this horizon (Unruh radiation).

The first new contribution of MiHsC is that it says Unruh radiation is damped between the object and the horizon. Ernst Mach said, 'what can't be seen, can't exist', so from the point of view of the object all fields beyond the horizon must be zero, so they must be zero on the horizon too. Therefore, only waves with nodes at the horizon can be allowed. This cuts out many Unruh waves on the left side but not on the right, so more Unruh radiation hits the object from the right, slowing its acceleration. This correctly models what we call inertia, which has never before been explained. In general the horizon makes the zero point field, hitherto hidden, suddenly vary in space and able to push on real objects (see reference McCulloch, 2013, below).

The second part of MiHsC is that the Unruh radiation is also damped slightly by the far off Hubble horizon which cuts out some long wavelength Unruh radiation. This weakens the part of MiHsC described above, and so weakens inertia slightly in a new way. This makes more difference for low acceleration objects (which see long Unruh waves) and in this way MiHsC correctly models galaxy rotation without dark matter, and cosmic acceleration without dark energy (McCulloch, 2012).

Now to the emdrive: the photons in the cavity have inertial mass (photons in a mirrored box do) so MiHsC should apply. If we assume that the cavity walls are like the cosmic horizon in MiHsC then they will damp some Unruh radiation and make inertia weaker, but less so at the wider end. So the photons at the wide end have more inertia, and photons gain mass going from the narrow to the wide end. You'll note that mass-energy is not conserved in the usual way here because the horizon causes the zero point field to become real: just as black hole horizons cause virtual particles to become real (Hawking radiation). To conserve momentum the cavity has to move towards the narrow end. This predicts the emdrive results quite well, see here.

The application of MiHsC to the emdrive is summarised and derived properly (mathematically) in the paper below (McCulloch, 2015) and I'm mentioning it here in the hope of stimulating much needed debate.

References

McCulloch, M.E., 2013. Inertia from an asymmetric Casimir effect, EPL, 101, 59001. Link

McCulloch, M.E., 2012. Testing quantised inertia on galactic scales. Astrophys. and Space Sci., 342, 2, 575- Link

McCulloch, M.E., 2015. Can the emdrive be explained by quantised inertia. Progress in Physics, 11, 1, 78-80. Link

Re-Open the X-Files

A while ago now I tweeted the following: 'If you want to know how to do creative theoretical physics, then ignore today's mainstream & read about physicists from 1609 to 1930 and hold yourself to their standard'.

Consider the theoretical discoveries before 1930. In 1609 for example. Kepler looked at the new data on weird, sometimes retrograde, planetary orbits collected by Tycho Brahe and adopted the radical Copernican Sun-centred Solar system, ditched the complex epicycles and devised simpler equations to model planetary motions. Newton simplified further in 1687 by stealing orbital data from poor old Flamsteed at the Royal Observatory, and used the data to perfect his radical action-at-a-distance theory of gravity (and told a distraught Flamsteed to go 'bind his head with a garter'). In 1873, Maxwell, in a more kindly way, used Faraday's observations of electro-magnetism, which seemed magical at the time, to write down his new equations for light. In 1905, Einstein used the puzzling null result from the Michelson-Morley experiment and the photoelectric effect to propose the counter-intuitive special relativity and support Planck's bizarre quantum mechanics. In each case, strange new data from what you might call the 'X-files' was accepted & theories were rewritten, fundamentally, but in a way that didn't change the predictions for regimes already well explored.

In contrast, everything in mainstream fundamental physics since 1930 or so has been merely a logical extension of Einstein and his contemporaries. This is not for a lack of strange new data. We have had anomalies in deep space since Fritz Zwicky found in 1933 that galaxies in galaxy clusters were moving far too fast to be bound, as they obviously were. There was a similar finding that stars in galaxies were orbiting too fast by Vera Rubin in 1980. John Anderson found anomalous spacecraft tracks in the 1990s and 2000s and Reiss and Perlmutter discovered cosmic acceleration in the 2000s, and there are many more anomalies from deep space (eg: aligned quasars) and from laboratories (eg: Podkletnov, Tajmar, LENR, emdrive), but all this strange data, anomalies now apparently representing 96% of the mass-energy in the cosmos, have not been allowed to come in from the cold, and complex fixes involving invisible entities have been found to allow the old models to accommodate some of them (an exception is CERN where they are freer to move because no former great has laid down the law for this new high acceleration regime).

With MiHsC I have embraced these physics X-files and written new formulae that agree with the old physics at high accelerations, but, at low accelerations, or if horizons are brought closer, agree with the new data rather than the old physics. This data-driven method is as it should be, but I know that convincing others takes time and care, always has. What is needed is more than a proof that MiHsC predicts more simply, which I have already done, but a crucial experiment or anomaly that is impossible to explain any other way: ideally a controllable laboratory experiment involving extreme spin as suggested in my book (an experiment which is in progress) or an experiment like the emdrive (see my paper below).

I hear the X-files are coming back to TV. Despite the scientific flaws in those episodes, their scientific attitude was exactly right. As Carl Sagan once pointed out: you need a mix of scepticism (Scully) and curiosity (Mulder). Today, we need more Mulders.

Reference

McCulloch, M.E., 2015. Can the emdrive be explained by quantised inertia? Progress in Physics, Vol 11, Issue 1, 78-80. Link to pdf

MiHsC vs 29 anomalies

Someone pointed out to me this week that I tend to publish papers predicting one anomaly at a time with MiHsC (quantised inertia) and these are easy for others to discount, but a paper showing how MiHsC predicts all the anomalies would have more impact. MiHsC now predicts 29 anomalies quite well (and doesn't mess up non-anomalies). Of course, I have already published a book which presents most of the results together, but it's good to be succinct, so I have summarised all  my published results, and some as yet unpublished, in this Table (click on it for a closer look):

The second column identifies the anomaly, column 3 shows the size of the observed anomaly, column 4 shows the MiHsC prediction of it, and column 5 is a brief discussion of the degree of success of MiHsC, and also mentions rival hypotheses, their degree of success, and how arbitrary they are. I have arranged the anomalies from the cosmic scale down to the Planck scale. It is always risky putting something like this up, because there may be errors, and some may disagree with my assumed cosmic acceleration for example, but I'm putting it up so people can make comments and correct me if needed.

The main point here is that my confidence in MiHsC is not due to its agreement with any one anomaly, which is rarely perfect, but the generality of all of them together (Introduction to MiHsC).